乾燥空気の気体定数を求める
気体における圧力・密度・温度は密接に関連している。
初等力学において空気抵抗あるいは物体の損壊や回転等々を考慮しないように、気体の研究においてもその理論構成にあたっては、ある程度制約条件を設けるのが望ましい。これによって建立される概念が『理想気体』である。
理想気体とは端的に言えば状態方程式と呼ばれる関係式を完璧に満たすもののことであるが、厳密に言えばそれは『分子の体積がゼロ』で『分子間力がゼロ』という2条件に起因する。その条件から明らかなように、理想気体は存在しない。
下図の通り。但し、pは圧力、ρは密度、Tは絶対温度(ケルビン)を表す。Rは気体ごとに定まる定数で、気体定数という。記述としては『R(気体名)』と表示するのが適切だが、ここでは省略している。

気体定数を求める旅へ
気体は、大量の分子によって構成されている。
水蒸気はH2Oという分子の集合であるが、これらの動きをひとつひとつ捉えるのは現実的ではない。そこで我々が扱う単位を「分子ひとつずつ」からもう少し大きくすることを考える。この単位を1mol(モル)という。
1molは、分子を6.02 × 10^23(23乗)個集めたものである。
この塊を1単位として、気体を扱っていくことになる。
なぜこのような個数になったのかといえば、分子をこれだけ集めれば分子量という値と一致するからである。分子量は、炭素Cの質量を12であると決めてしまって、これと比較して当該分子または原子の質量を表示する方法である(原子の質量の場合は、原子量と呼ばれる)。
分子量については下図が成り立つ。:すなわち、H2Oの分子量は『Hの原子量+Hの原子量+Oの原子量』によって計算される。

例えば炭素Cの原子量は12だが、これを1mol集めると12グラムになる。
このような1molあたりのグラム数をモル質量という。1molというまとまりが基本単位であることを思い出そう。モル質量の値は、分子量の値と等しい。
単位はg/mol。molを掛ければgが出てくる。
次はキロモル数を定義しよう。kmolと書く。グラムをキログラムに直したのと同じように、1kmol=1000molである。これを一般的に表現すれば、次のようになる。

当然、1(g/mol)は、1000分の1(kg/mol)であることを確認しておく。
さて、分子量がM。つまりM(g/mol)の気体をm(kg)=1000m(g)とるとする。
このとき、1/M(mol/g)に、1000m(g)を掛けると、1000×(m/M)molとなる。
ここでnキロモル(kmol)を上図のように定義すれば、nキロモル=1000nモル □
ごく簡単にいえば、1キロモルとは1モルを1000セット持ってきたものである。
1モルというのは6.02×10^23(23乗)個の分子を集めたものだった。当然二つの異なる気体から『1モルを取ってきます』といえば、それぞれの気体に含まれる分子の数は等しくなる。分子の数が等しい気体は、同圧力・同温度にすると、それがたとえどんな気体でも同じ体積を持つようになる……というアボガドロの法則が利用できる。

(p:圧力、R:気体定数、ρ:密度、T:絶対温度、m:質量)
状態方程式を変形すると、上図のようになる。
いま気体が同圧力・同温度であるとするとアボガドロの法則より同体積でもあることがわかる。すると最終式の左辺はその状況下では一定の値を取り続けるだろう。この一定の値をR*とおけば、R*=R×mとなる。
いま、気体を1キロモルだけ取って来ていたことを思い出せば、1=m/Mであり、m=Mであることもわかるから、
R*=RM
が導出されるわけである。
これまでの議論の流れは、
(1)ある気体をいい感じの量持ってくる。 ← 1キロモル
(2)同圧力・同温度にしてやると、同体積になる ←アボガドロの法則
(3)R*=RM
だった。これによって、大気の研究をするうえで基礎となる水蒸気の含まれていない乾燥空気の気体定数を具体的に求めることができる。上と同じような流れで実験すれば定数が求まることを理論が保証してくれたと見ると、ものすごく気持ちが良い。
さて、にんじんは実験には興味がないから、実験結果を見てみよう。
T=273.15ケルビン、p=1013.25hPaの環境を用意してやる。そこで1キロモルの乾燥空気の体積は22.4135立方メートルだということが実験により確認されたので、
R*= 8.3143×10^3
であることがわかった。
あとは乾燥空気の分子量が求まればよいことになる。
乾燥空気は、様々な気体の混合物である。我々はつい先ほどまで「単一の気体」を前提に話を進めて来たのだった。式の変形に状態方程式を用いているが、混合気体にも状態方程式は成立するのだろうか? まずこのことを確認しよう。
我々はその混合物が何個あるのだか知らない。しかし有限個であることは前提してよいと思われるので、n種類の気体の混合であるとしよう。気体を適当にリストにして、i番目にある気体について考えよう。当然これも気体であるから、状態方程式が成立している。
また、ダルトンの法則によれば、混合気体の圧力は各成分の圧力の和に等しい。
この二つの事実から、
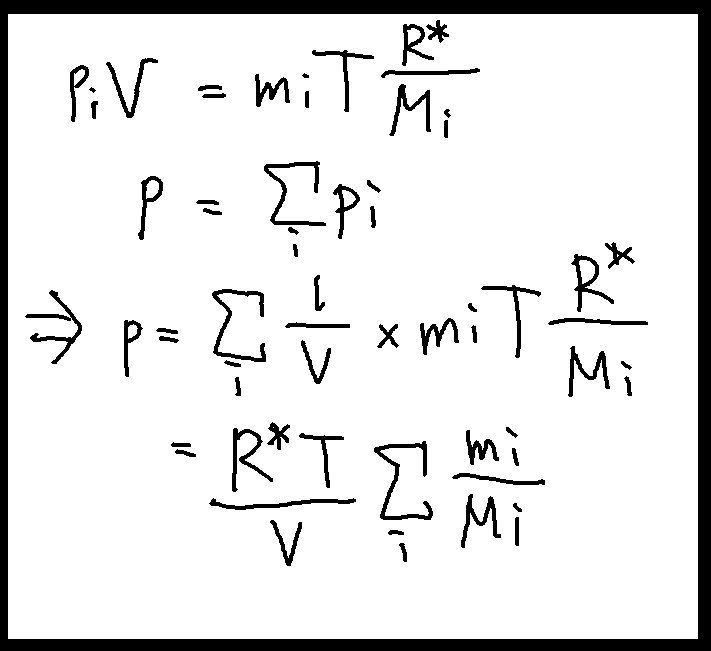
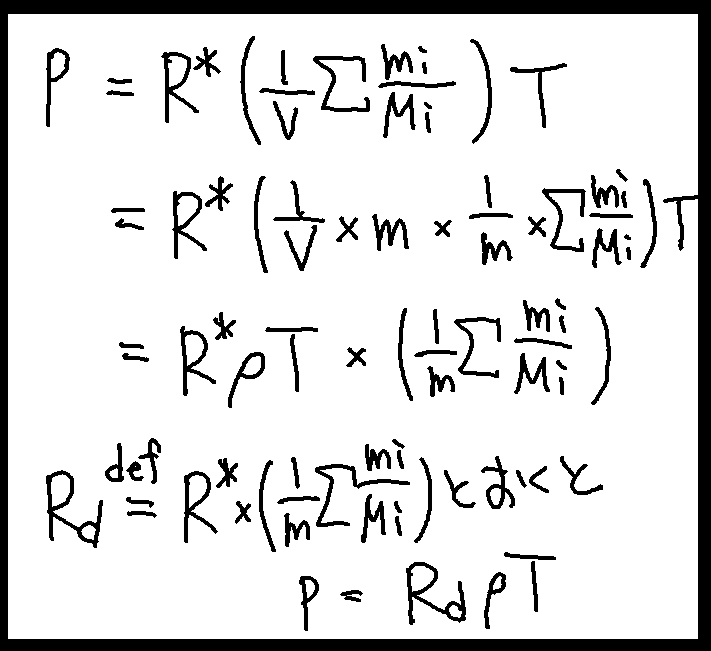
となり、p=R(d)ρTとなり、混合気体に対しても状態方程式が成立することがわかった。そうすると、単一の気体と同じように式変形を施すことができる。
乾燥空気に含まれる気体がどれぐらいあって、どれぐらい分子量を持っているのか。これについては実験してみなければわからない。……というわけで実験してもらうと、いくつかの気体がリストアップされ、それぞれの分子量が求まる。
つまり、各Miの値が理解されたわけである。
1キロモルの気体といったとき、質量は明確ではない。だからmiの値は決められない。そこで、1キロモルの気体を1kgとってくるものと仮定しよう。
このとき、
1kgの乾燥空気に対する気体定数Rdは、
Rd = 287
と求めることができる。
海面補正が自分でできるようになる
今回は高度が上がるにつれて、大気の圧力や密度がどう変化するのかを調べる。
以前書いたものをより精緻にする作業でもある。
次の図は単位面積1平方メートルの鉛直方向にある気柱である。

高さzと、高さz+Δzを区切りにした空気塊を水色で表示している。この空気塊の密度をρとしよう。体積はΔzであるから、その質量はρΔzとなり、空気塊自体にかかる力は重力加速度gを用いて、gρΔzと表される。
z+Δzの水平面にかかる力をp1、zの水平面にかかる力をp2としよう。この空気塊は移動せず釣り合っている(静力学平衡)ことから、以上の三つの力について次の関係式が成り立つ。
p1+gρΔz = p2
変形すれば、
p1-p2 = -gρΔz
ここに乾燥空気の状態方程式を当てはめると次のようになる。
記号が煩雑なら、p2を単なるpに、p1-p2をΔpとおけば右図のようになる。
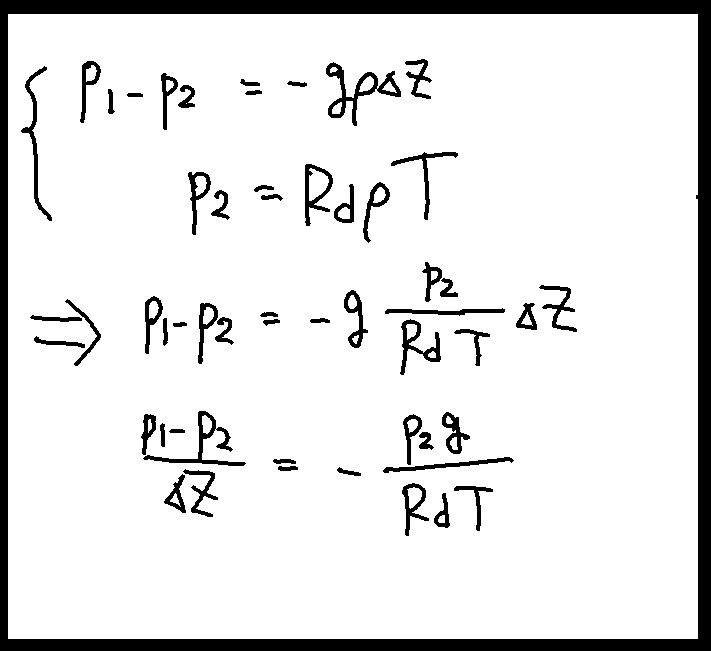
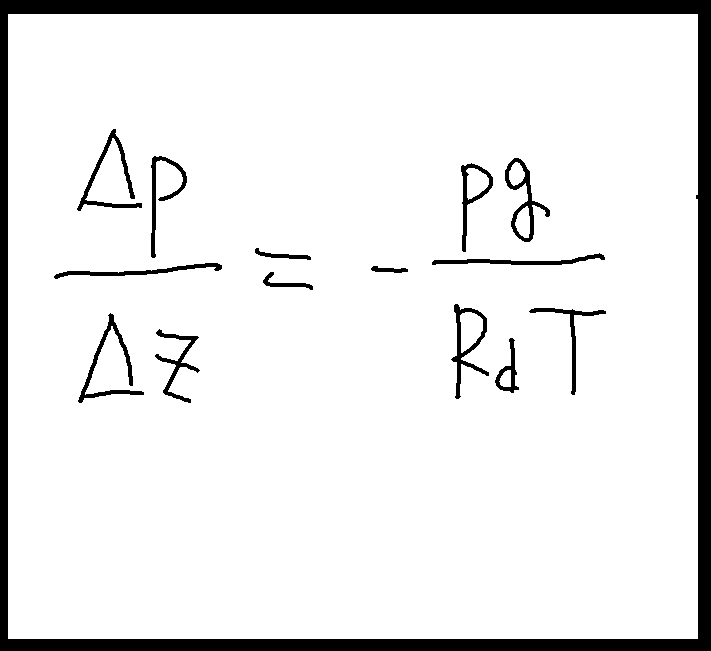
海面補正
これによって「海面補正」という操作がわかりやすくなる。
気圧というものは高さを上げるほど減っていく。だから本来は基準となる高さ(海面)で観測するのが理想だが、地形的な問題もあって、それがいつも実現できるとは限らない。そこで、観測所の高さを考慮し、補正を加えて、海面で測定したときの数値を求めることを考える。
たとえば、海抜500mで測定したとしよう。気圧は940hPa、気温は15℃だった。
これをもし、海抜0mに直せば、この数値はどう変わるだろうか?
但し、大気の温度は100mにつき、0.65℃減少していくとする。
但し書きより、海面における気温は18.25℃である。
下図、空気塊(箱の部分)の平均気温は、(15+18.25)/2で、約16.6℃になる。これは約289.8ケルビンに相当する*1。
- p=940×100
- g=9.81
- Δz=500
- Rd=287
- T=289.9
という数値を先ほどの式に放り込めば、Δpの値が55.43hPaと出る。Δpは気圧差だったから、海面での気圧は940hPaから55.43hPaを引いた値である995.4hPaになる。
 □
□
という具合で、海面補正ができる。
しかし、厳密に言えば500mと幅のある空気塊で考えると、「平均気温が約16.6℃だ」というのはなかなか乱暴な話だともいえる。だから500mではなく、たとえば100mずつで区切って、少しずつ海抜0mの位置に下がって来ることが望ましい。
海面補正が自分たちにもできるようになったのだ!٩꒰๑╹ω╹๑ ꒱۶
[おまけ]
基本はこれでいいのだが、しかし、100mずつの空気塊でも相当乱暴だともいえる。
そういう人々のために「積分」がある。積分は「100mずつ」ではなく、これを可能な限り無限に細かく分割するやりかたである。下図を見た時に「微分」が連想できる人のやり方だから特に気にする必要もないが、積分を勉強するときに思い出すと一応、あの積分という概念が理論的に役立っていることがわかる。
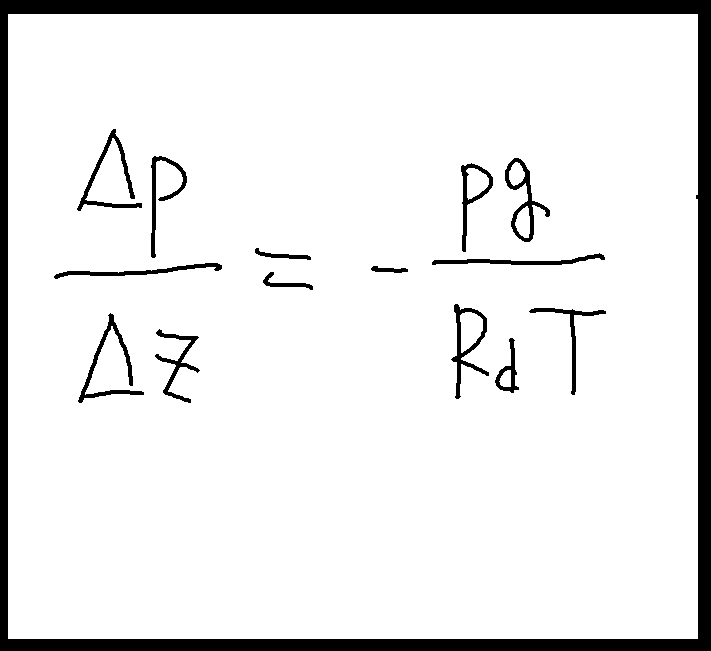
これを微分の形に直すと次のようになる(下図左)
注意しなければならないのは、zに応じて変化するのはpだけではなく、Tもそうだということである。だから厳密にいえば、下図右のように書くのがわかりやすい。この式から高度に応じた気圧、即ちp(0)を求めるにはこの微分方程式を解く必要がある。そして微分方程式を解くためには「積分」がいる、という次第である。
ちなみにT(z)=0、すなわち0Kとなること(絶対零度)はない。それが仮定である。現実的にも0Kになることはまったくない。
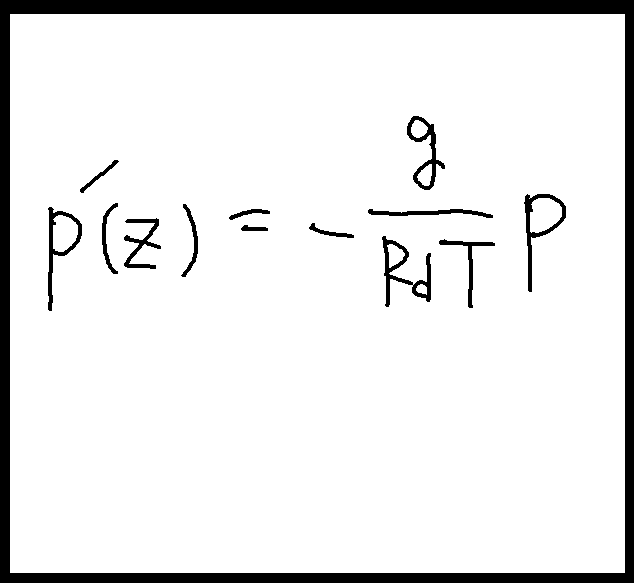
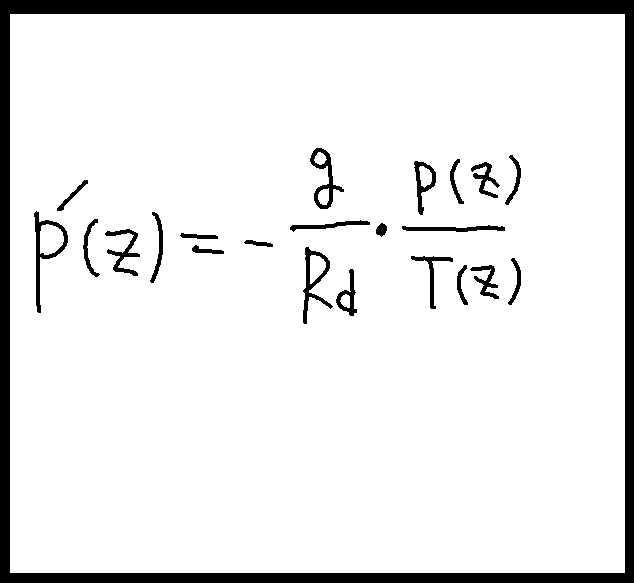
これは斉次一階線形微分方程式だから比較的簡単に解ける。
うるさいようだが、下図の二番目の変形でp(z)を分母に持ってきているのは、少なくとも0~500mの間でp(z)が0になることはないからである

これを計算していくと、

こう計算して、下図に行きつく。
あとはp(0)以外の値を全部入れてやればp(0)=996.2hPaと出る。500m区切りでやった方法では995.4hPaだったから1000Pa以上違うことになるわけだ。

♪L( ^ω^ )┘ 疲れた └( ^ω^ )」♪
おわりに
今回のポイントは「静力学平衡状態の状態方程式」である。
静力学平衡であれば状態方程式に高さが導入でき、それを利用して海面補正、広くは、高度と気圧の関係について議論することができるという部分が重要だと思う。
前回の「大気の熱力学入門記事」では気体定数を求めることを行った。そしてそこでも主題となっていたのは状態方程式であり、特に混合気体についての状態方程式である。1キロモルという話もあったが、分子量=質量にしてやろうという理論的・技術的なテクだとみれば、今回も結局は状態方程式いじりの一環であった。

図解・気象学入門―原理からわかる雲・雨・気温・風・天気図 (ブルーバックス)
- 作者: 古川武彦,大木勇人
- 出版社/メーカー: 講談社
- 発売日: 2011/03/23
- メディア: 新書
- 購入: 3人 クリック: 24回
- この商品を含むブログ (10件) を見る
熱力学の第一法則
次に考えるのは「内部エネルギー」である。
これは物体の運動エネルギーや位置エネルギーという力学エネルギーを取り去ったあと、物体に残っているとするエネルギーのことである。即ち、たとえ動いていなくても、高い位置になかったとしても、その物体にはエネルギーがあると考えるのである。
そもそもエネルギーとはなんだろうか?
ある物体に力Fニュートンを加えた時、物体が力の方向にLメートルだけ動いたとする。このとき、この力はFLジュールだけ仕事をしたと言われる。ジュールとはニュートン×メートルのことであるから、あまり気にしなくてよい。問題はこの「仕事」である。
エネルギーとは、仕事をする能力のことである。
たとえば時速100kmで車を走らせて、人形を轢いたとしよう。速度がはやければはやいほど遠くまで人形は弾き飛ばされるだろうし、これより速度が多少遅かったとしても、普通の乗用車よりも2トントラックに轢かれるほうが人形に与える影響は大きい。
単に高い位置にあるというだけでも、仕事をする能力がある。金ダライを高くから落とせば落とすほど、下のものに与える影響は大きい。
しかし運動していなくても、高い位置になくても、物体は仕事することができる。その例は既に、雲の形成のところで触れてある。即ち、空気塊は上昇するとその体積を増やす。体積を増やすということは、空気塊に触れた他の部分を押しのけるということである。このことからしても、内部エネルギーというものを考えるのは妥当といえる。
内部エネルギーというものについて考える時、基本となるが「熱力学の第一法則」である。力学的エネルギーと同様に、内部エネルギーというものも変化の前後でその総量は変わらない。
ΔQという量の熱を加えよう。もともとの物体にはU1という内部エネルギーがあるとする。もちろん、内部エネルギーの中身は今のところまったくわからない。そして、たとえば湯気が出てくると鍋のフタがカタカタと動き始める。即ち仕事をするのであるが、この仕事の量をΔWとする。そしてあとの状態の内部エネルギーをU2とすれば、
ΔQ+U1 = ΔW+U2
となっている。これが熱力学の第一法則である。当然のことではあるが、エネルギーというものはすべて仕事に使われない。自動車が人形に激突しても人形を吹き飛ばすために全精力を傾けはせず、少し速度が落ちるが、そのまま走り続けるのと同じである。
ΔUとしてU2-U1と定義すれば、
ΔQ = ΔW+ΔU
とも表現できる。

※熱とは、エネルギーの流出又は流入のことで、単に加熱するというだけではないことに注意を要する。温かい物体の上に冷たい物体を置いておくと、冷たい物体は次第に温度が上がる。
ΔQ=ΔW+ΔUだから、仕事をすれば(ΔW>0)熱が出る(ΔQ>ΔU≧0)。
内部エネルギーというものは、第一法則をもとに、その変化について扱われる。換言すれば、「今この物体は内部エネルギーを〇〇だけ持っている」というよりは、「この変化によってこの物体の内部エネルギーは〇〇だけ増えた」というような言い方で取り扱われるということである。
この内部エネルギーの変化というものが、実は温度だけに依存することを示したのは物理学者のジュールであった。温度がΔTだけ変化したときの内部エネルギーの変化ΔUは、
ΔU = Cv × ΔT
と書き表せる。(Cvは定数。気体によって変わる。)
すなわち、熱力学の第一法則における式はこれを用いて、
ΔQ = ΔW+CvΔT
となる。
おまけ(定圧比熱)
さて、球形をした空気塊を考えよう。この空気塊の圧力はp、表面積はAとする。
圧力とは単位面積当たりの力であったから、球体の表面に衝突する空気の力がpAニュートンであることはすぐにわかる。もしこの力によって空気塊が半径Δrだけ膨らんだとすると、pAニュートンがした仕事の量ΔWは、pAΔrジュールということになることは、先ほどの定義の通りである。
このΔrが極めて微小であるときに限るが、この半径の変化による空気塊の体積の変化ΔVはAΔrと書くことができる。何故ならΔrの値が小さいので、(Δr)^2、(Δr)^3といった数はほとんど無視できるほど小さくなるからである。
したがって、ΔW = pAΔr = pΔV という式が成立する。
さらに、熱力学の第一法則より、次式が成立する。:
ΔQ = pΔV+CvΔT
空気塊は膨らむことによって圧力をΔp、温度をTからΔTだけ変化させたとしよう。
いまこの時の状態方程式は、

である。これを整理すると、

こうなる。ズルいのは、ΔpとΔVがpやVよりもずっと小さいとして、ゼロに近似しているところである。ものすごい勢いで膨らんだときのことを一切考えていないのは、今の目的があくまで定数を求めることであるから。それに都合の良い状況設定を考えているのだ。
以上より、次の2式がわかった。

これより、

Δp=0となるように、つまり圧力一定になるように空気塊を膨らませると、
ΔQ = (R+Cv)ΔT となる。
つまりR+Cvが定圧状態における定数ということがわかる。

図解・気象学入門―原理からわかる雲・雨・気温・風・天気図 (ブルーバックス)
- 作者: 古川武彦,大木勇人
- 出版社/メーカー: 講談社
- 発売日: 2011/03/23
- メディア: 新書
- 購入: 3人 クリック: 24回
- この商品を含むブログ (10件) を見る
*1:小数第一位以下は省いています。詳しくは「有効数字」


